AI Weekly Report Primer

By Turing

Neurosymbolic AI

1. Introduction

Artificial Intelligence (AI) has made remarkable progress in recent years with breakthroughs in various domains such as computer vision, natural language processing, and robotics. However, despite the impressive achievements of deep learning and other neural network approaches, there are still significant limitations in terms of interpretability, generalizability, and reasoning capabilities. Neurosymbolic AI (NAI) has emerged as a promising direction to address these limitations by combining the strengths of both neural networks and symbolic AI techniques.

NAI is an interdisciplinary field that aims to integrate the learning and representation capabilities of neural networks with the reasoning and abstraction capabilities of symbolic AI. The goal is to create AI systems that can learn from data, reason about complex concepts, and make decisions in a way that is both flexible and interpretable. By bringing together the best of both worlds, Neurosymbolic AI has the potential to unlock new possibilities in AI and enable the development of more robust, explainable, and trustworthy AI systems.

The importance of NAI lies in its ability to address some of the key challenges facing current AI systems. For example, deep learning models are often criticized for being “black boxes” that are difficult to interpret and explain. NAI can help to make these models more transparent by incorporating symbolic knowledge and reasoning capabilities. Additionally, NAI can enable AI systems to generalize better to new situations and tasks by leveraging abstract knowledge and reasoning.

NAI has a wide range of potential applications across various domains. In natural language processing, it can enable more accurate and efficient question answering, dialogue systems, and language understanding. In computer vision, it can improve object recognition, scene understanding, and visual reasoning. In robotics and autonomous systems, it can enable more flexible and adaptive decision-making and control. Other potential applications include healthcare, finance, and education.

In the following sections, we will delve deeper into the foundations, architectures, and applications of NAI. We will explore the key concepts and techniques that underlie this exciting field and discuss the challenges and opportunities that lie ahead.

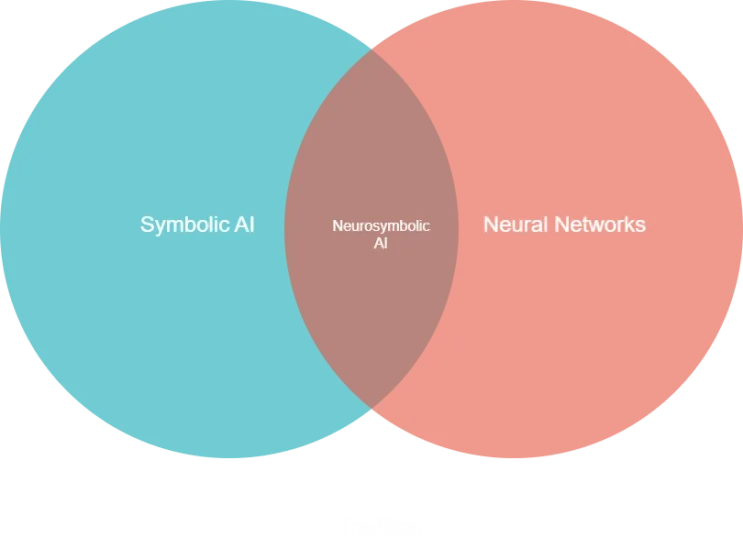Diagram 1. The intersection of Symbolic AI and Neural Networks

Diagram 2. Integration of Neural Networks and Symbolic AI rulesets

The following table shows the strengths and weaknesses of both approaches. The advantage of NAI is that each component can complement the other to achieve a much more effective system.

Table 1. Comparison of Symbolic AI and Neural Networks

Aspect	Symbolic AI	Neural Networks	Neurosymbolic AI Integration
Knowledge Representation	Strengths: - Explicit and interpretable knowledge representation - Ability to encode domain knowledge, rules, and constraints Weaknesses: - Difficulty in capturing complex and nuanced knowledge - Knowledge acquisition bottleneck	Strengths: - Ability to learn complex and nuanced patterns from data - Automatic feature learning and representation Weaknesses: - Lack of explicit and interpretable knowledge representation - Difficulty in incorporating domain knowledge and constraints	- Symbolic knowledge provides interpretability and explicit representation - Neural networks learn complex patterns and features from data - Integration allows for capturing both explicit and implicit knowledge
Reasoning and Inference	Strengths: - Logical and rule-based reasoning - Ability to perform explainable inference Weaknesses: - Brittleness and lack of robustness to noise and uncertainty - Difficulty in handling ambiguity and common-sense reasoning	Strengths: - Robust and flexible reasoning based on learned patterns - Ability to handle noise, uncertainty, and ambiguity Weaknesses: - Lack of explainable and interpretable reasoning - Difficulty in incorporating logical rules and constraints	- Symbolic reasoning provides explainable and rule-based inference - Neural networks enable robust and flexible reasoning - Integration allows for handling both logical and common-sense reasoning
Generalization and Adaptability	Strengths: - Ability to generalize based on explicit rules and knowledge - Interpretable and controllable generalization Weaknesses: - Limited generalization beyond the encoded knowledge - Difficulty in adapting to new situations and data	Strengths: - Excellent generalization ability based on learned patterns - Adaptability to new situations and data through learning Weaknesses: - Overfitting and poor generalization if not properly regularized - Difficulty in generalizing to out-of-distribution data	- Symbolic knowledge provides interpretable and controlled generalization - Neural networks enable adaptability and generalization to new data - Integration allows for robust and explainable generalization
Scalability and Efficiency	Strengths: - Efficient inference based on symbolic reasoning - Scalability to large knowledge bases Weaknesses: - Difficulty in scaling to complex and large-scale problems - Computational complexity in reasoning and inference	Strengths: - Scalability to large datasets and complex problems - Efficient learning and inference through parallel processing Weaknesses: - High computational requirements for training and inference - Scalability challenges for very large neural networks	- Symbolic reasoning provides efficient inference for large knowledge bases - Neural networks enable scalability to complex and large-scale problems - Integration allows for balancing computational efficiency and complexity

2. Brief History of AI

The field of AI has evolved significantly since its inception in the 1950s. Early AI research focused on symbolic approaches such as the General Problem Solver (GPS) and the Logic Theorist, which aimed to solve problems using symbolic reasoning and heuristic search. In the 1960s and 1970s, expert systems emerged as a prominent application of symbolic AI, using rule-based reasoning to emulate the decision-making of human experts in various domains.

However, symbolic AI approaches faced several challenges, such as the difficulty of capturing common-sense knowledge and the brittleness of rule-based systems. In the 1980s, the focus shifted towards neural networks inspired by the structure and function of biological neurons. The development of backpropagation algorithms enabled the training of multi-layer neural networks, leading to significant advances in pattern recognition and machine learning.

The 1990s and 2000s saw the rise of machine learning techniques such as support vector machines and ensemble methods, which demonstrated impressive performance on various classification and regression tasks. However, the real breakthrough came in the 2010s with the advent of deep learning, powered by the availability of large datasets, powerful computing resources, and advanced neural network architectures like convolutional neural networks (CNNs) and recurrent neural networks (RNNs).

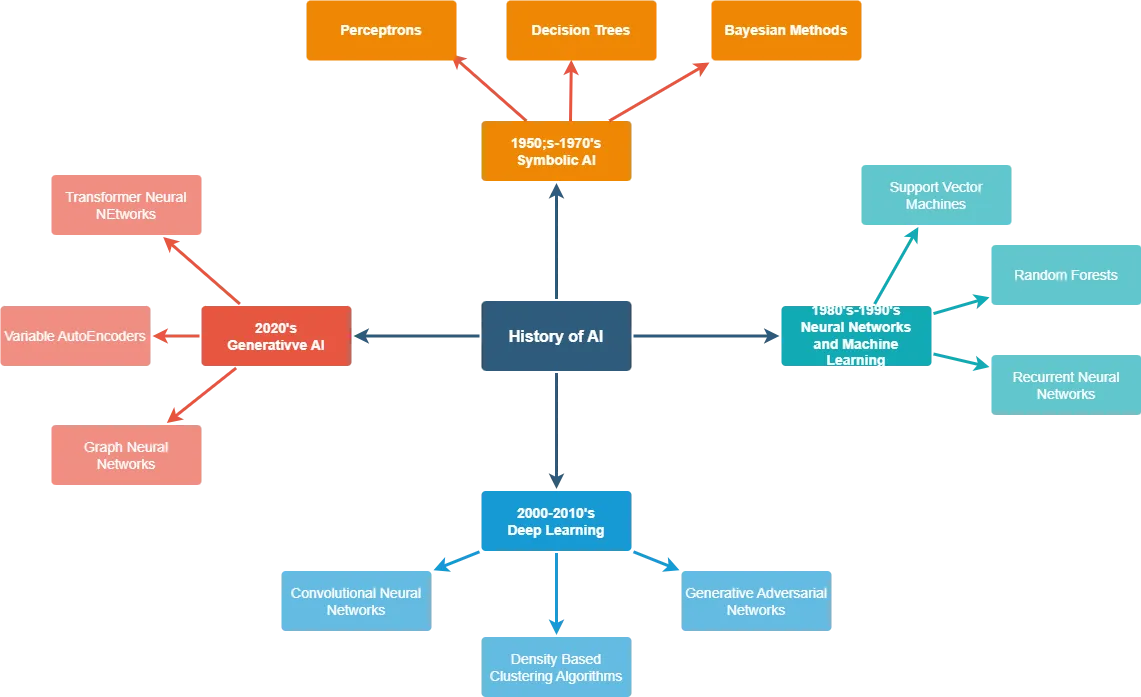Diagram 3. A brief history of AI development

2.1 Limitations of Traditional Symbolic AI and Neural Networks

Despite their significant contributions to AI, both symbolic AI and neural networks have their own limitations.

Symbolic AI Approaches Struggle with Several Issues:

Knowledge acquisition bottleneck: Encoding expert knowledge into rules is time-consuming and labor-intensive.
Brittleness: Symbolic AI systems are often brittle and fail to handle situations that deviate from their predefined rules.
Scalability: As the complexity of the problem increases, the number of rules required grows exponentially, making it difficult to scale symbolic AI systems.
Lack of learning: Traditional symbolic AI systems do not improve with experience and cannot learn from data.

Neural Networks, While Powerful Learners, Also Have Limitations:

Interpretability: Deep neural networks are often considered “black boxes,” making it difficult to understand how they arrive at their decisions.
Data dependency: Neural networks require large amounts of labeled data for training, which can be expensive and time-consuming to acquire.
Generalization: Neural networks can struggle to generalize to new situations that differ significantly from their training data.
Robustness: Neural networks can be vulnerable to adversarial attacks, where small perturbations to the input can lead to incorrect predictions.

2.2 Need for Integrating Symbolic and Neural Approaches

The limitations of symbolic AI and neural networks have motivated researchers to explore ways to integrate the two approaches, giving rise to the field of Neurosymbolic AI. By combining the strengths of both approaches, Neurosymbolic AI aims to create AI systems that are:

Interpretable: Incorporating symbolic knowledge and reasoning can make the decision-making process of neural networks more transparent and explainable.
Data-efficient: Leveraging prior knowledge and symbolic reasoning can reduce the amount of labeled data required for training neural networks.
Generalizable: Combining symbolic abstractions with neural network learning can enable AI systems to generalize better to novel situations.
Robust: Integrating symbolic reasoning with neural networks can improve the robustness of AI systems against adversarial attacks and out-of-distribution inputs.

Neurosymbolic AI approaches have shown promising results in various domains such as visual question answering, natural language processing, and robotic planning. By combining the learning capabilities of neural networks with the reasoning and abstraction capabilities of symbolic AI, Neurosymbolic AI has the potential to create more powerful, interpretable, and reliable AI systems.

3. Foundations of Neurosymbolic AI

Neurosymbolic AI builds upon the foundations of both symbolic AI and neural networks. In this section, we will explore the key concepts and techniques from each field that contribute to the development of Neurosymbolic AI systems.

3.1 Symbolic AI Techniques

Symbolic AI relies on explicit representations of knowledge and logical reasoning to solve problems. Some of the key techniques used in symbolic AI include:

Logic: Formal languages such as first-order logic and description logic are used to represent knowledge and perform logical inference.
Knowledge Representation: Techniques like ontologies, semantic networks, and frames are used to structure and organize knowledge in a way that facilitates reasoning.
Reasoning: Symbolic AI employs various reasoning methods such as deductive reasoning, inductive reasoning, and abductive reasoning to draw conclusions from available knowledge.
Search: Heuristic search algorithms such as A* and minimax are used to efficiently explore large problem spaces and find optimal solutions.

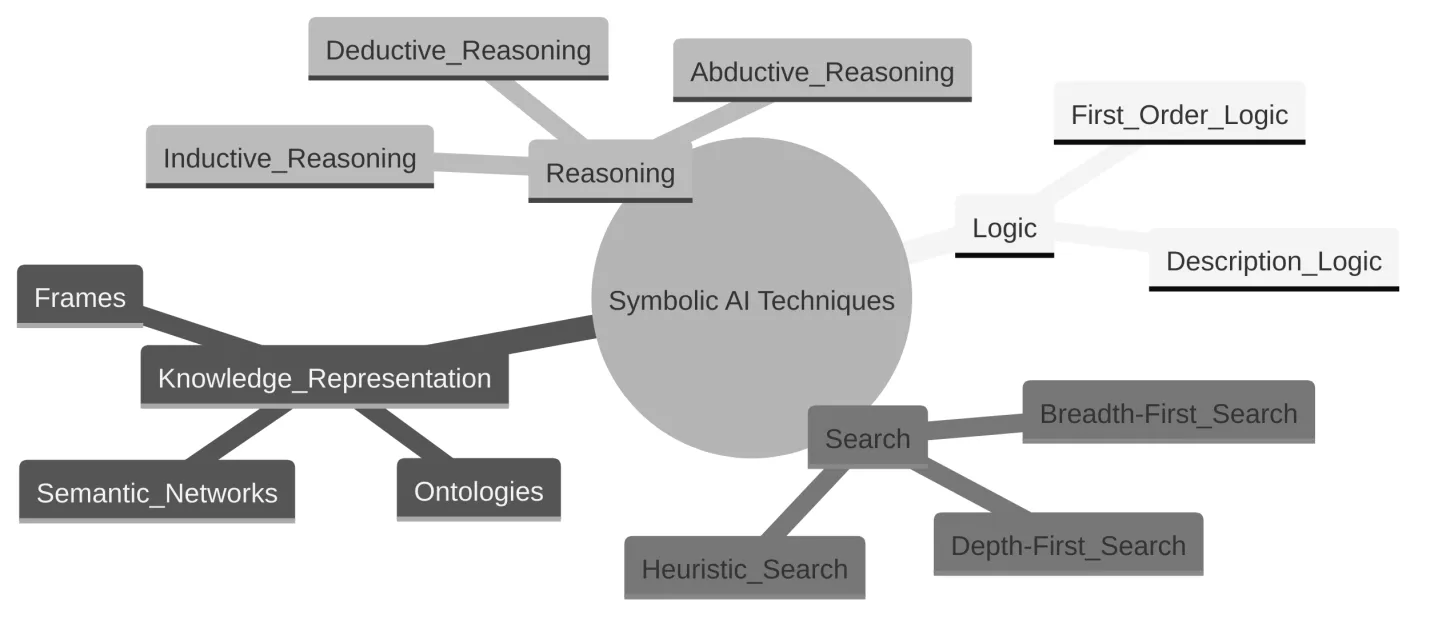Diagram 4. Symbolic AI techniques

3.2 Neural Networks

Neural networks are inspired by the structure and function of biological neurons and are capable of learning complex patterns from data. Some of the key concepts and techniques in neural networks include:

Artificial Neurons: The basic building blocks of neural networks, artificial neurons receive inputs, apply weights, and produce an output based on an activation function.
Network Architectures: Various neural network architectures such as feedforward networks, convolutional neural networks (CNNs), and recurrent neural networks (RNNs) are used for different types of tasks and data.
Learning Algorithms: Neural networks learn from data using algorithms like backpropagation, which adjusts the weights of the connections between neurons to minimize a loss function.
Representation Learning: Neural networks can automatically learn useful representations of input data, which can be used for various downstream tasks.

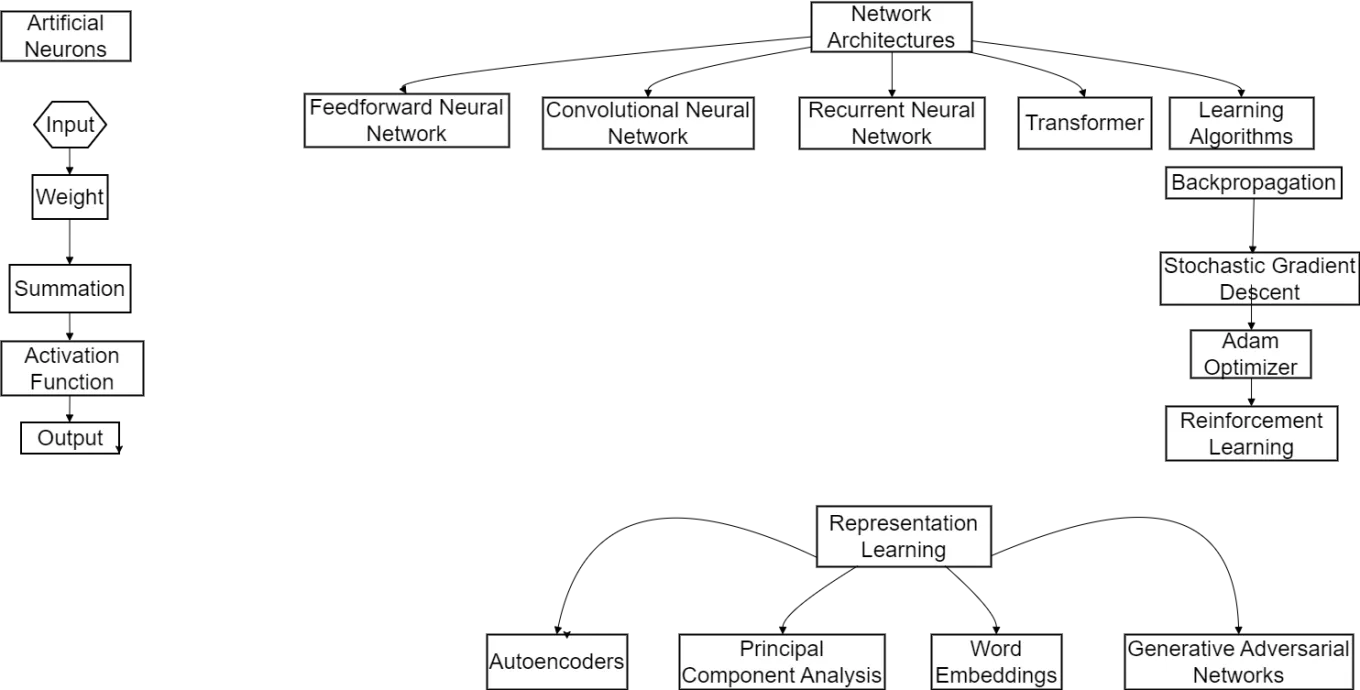Diagram 5. Neural Network Techniques

3.3 Advantages of Combining Symbolic and Neural Approaches

By combining symbolic AI and neural networks, Neurosymbolic AI aims to leverage the strengths of both approaches while mitigating their weaknesses. Some of the key advantages of this combination include:

Interpretability: Incorporating symbolic knowledge into neural networks can make their decision-making process more transparent and explainable.
Reasoning: Neurosymbolic AI systems can perform logical reasoning over learned representations, enabling them to draw conclusions and make inferences.
Data Efficiency: Leveraging prior knowledge and symbolic reasoning can reduce the amount of labeled data required for training neural networks.
Generalization: Combining symbolic abstractions with neural network learning can enable AI systems to generalize better to novel situations.

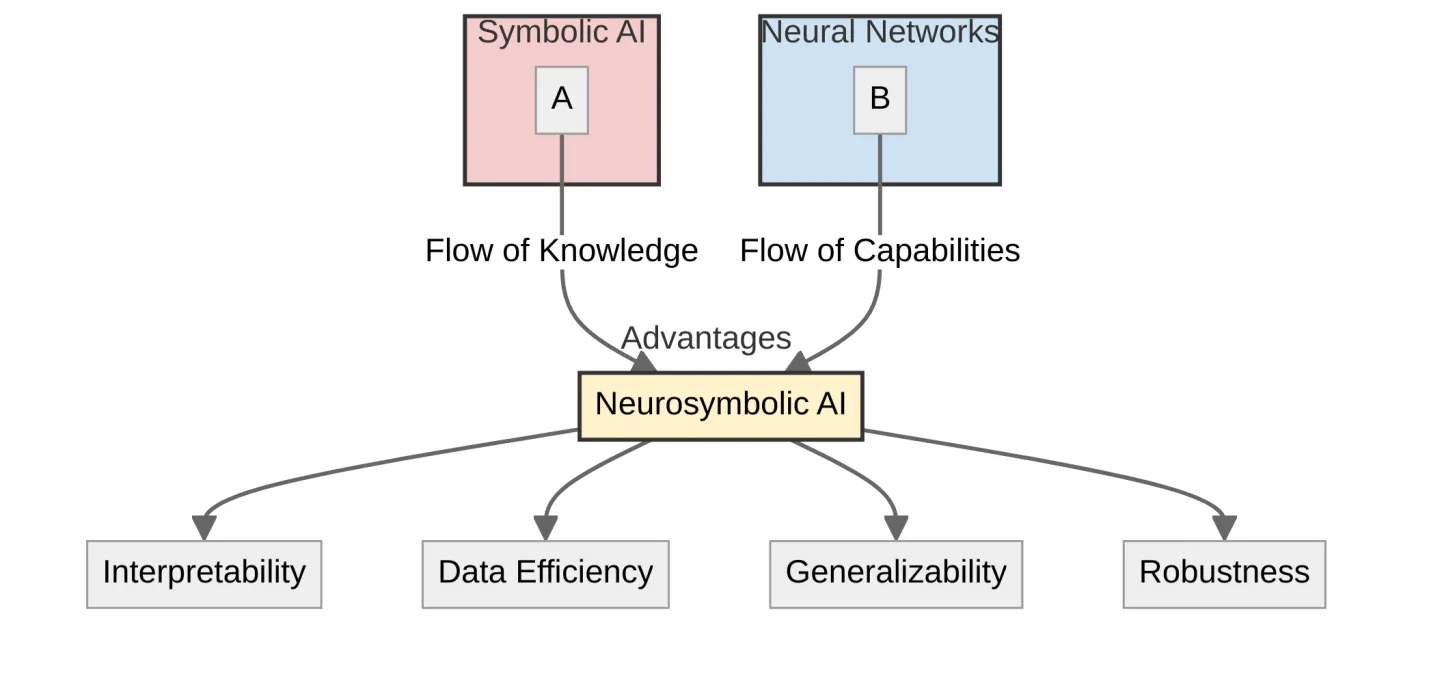Diagram 6. Integrating Symbolic AI and Neural Networks

3.4 Knowledge Graphs

Knowledge graphs are a powerful tool for representing and organizing structured knowledge in a machine-readable format. They consist of entities (nodes) and relationships (edges) between them, forming a graph-like structure. In Neurosymbolic AI, knowledge graphs can be used to:

Integrate symbolic knowledge with neural networks by embedding entities and relations into a continuous vector space.
Enable neural networks to perform reasoning over structured knowledge by propagating information through the graph.
Provide a unified representation for multi-modal data such as text, images, and videos by linking them to entities in the knowledge graph.

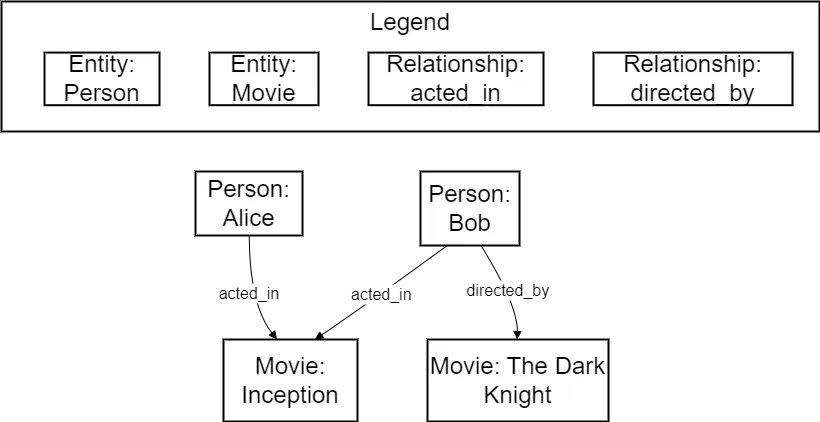Diagram 7. Example of a Knowledge Graph

3.5 Neuro-Symbolic Reasoning

Neuro-symbolic reasoning is a key aspect of Neurosymbolic AI that combines the strengths of neural networks and symbolic reasoning. Some of the techniques used in neuro-symbolic reasoning include:

Neural Theorem Provers: These models use neural networks to learn how to prove mathematical theorems by embedding logical formulas into a continuous vector space and performing reasoning over the embeddings.
Neural Symbolic Machines: These architectures integrate neural networks with symbolic programs, allowing them to learn and execute symbolic rules while leveraging the learning capabilities of neural networks.
Differentiable Reasoning: This approach makes the reasoning process differentiable, enabling end-to-end training of neural networks with symbolic reasoning components using gradient-based optimization.

3.5.1 Neural Theorem Provers

Neural Theorem Provers (NTPs) are a class of machine learning models that combine neural networks with symbolic reasoning to perform automated theorem proving. They aim to bridge the gap between the expressive power of neural networks and the logical reasoning capabilities of traditional theorem provers. Let’s explore Neural Theorem Provers in detail:

3.5.1.1 Overview

Neural Theorem Provers leverage neural networks to guide the search for proofs in a symbolic reasoning system. They learn to generate proof steps or select relevant axioms and rules based on the input problem and the current proof state. NTPs can be trained on large datasets of mathematical proofs and can generalize to unseen problems.

3.5.1.2 Architecture

NTPs typically consist of two main components: a neural network and a symbolic reasoning engine. The neural network acts as a guidance mechanism, suggesting promising proof steps or selecting relevant axioms and rules. The symbolic reasoning engine performs the actual logical inference and proof construction based on the guidance from the neural network. The architecture may vary depending on the specific implementation, but common approaches include graph neural networks, transformers, and attention mechanisms.

3.5.1.3 Training

NTPs are trained on datasets of mathematical proofs, which include the problem statements, axioms, rules, and the corresponding proof steps. During training, the neural network learns to predict the most promising proof steps or select relevant axioms and rules based on the input problem and the current proof state. The training objective is often formulated as a sequence-to-sequence problem, where the input is the problem statement and the output is the sequence of proof steps. Techniques such as supervised learning, reinforcement learning, or unsupervised pre-training can be used to train NTPs.

3.5.1.4 Inference

During inference, an NTP takes a new problem statement as input and aims to generate a valid proof. The neural network component suggests promising proof steps or selects relevant axioms and rules based on the learned patterns and the current proof state. The symbolic reasoning engine applies the selected axioms and rules to construct the proof, ensuring logical consistency and validity. The inference process iteratively combines the neural network’s suggestions with the symbolic reasoning until a complete proof is found or a certain depth limit is reached.

3.5.1.5 Advantages

NTPs can learn from large datasets of proofs and generalize to unseen problems, potentially discovering new proofs or shortcuts. They can handle complex and high-dimensional input spaces, such as mathematical formulas or structured data. NTPs can be more efficient than traditional theorem provers by leveraging the learned guidance from the neural network. They have the potential to combine the strengths of neural networks (pattern recognition, generalization) with the strengths of symbolic reasoning (logical consistency, interpretability).

3.5.1.6 Challenges and Limitations

Ensuring the correctness and soundness of the generated proofs is a critical challenge, as NTPs may produce logically inconsistent or invalid proofs. NTPs often require large amounts of training data in the form of annotated proofs, which can be expensive and time-consuming to obtain. The interpretability of the learned proof strategies and the reasoning process of NTPs can be limited, making it difficult to understand and trust the generated proofs. Scaling NTPs to handle very large and complex problems remains a challenge, as the search space for proofs can grow exponentially.

3.5.1.7 Applications

NTPs have been applied to various domains, including mathematics, formal verification, and program synthesis. They have shown promising results in automated theorem proving tasks, such as solving problems from university-level mathematics courses. NTPs can be used to assist human mathematicians in discovering new proofs or verifying existing ones. They have the potential to accelerate the process of formal verification in software and hardware systems.

Neural Theorem Provers represent an area of research that combines the power of neural networks with symbolic reasoning. While they have shown promising results, there are still significant challenges to overcome, such as ensuring the correctness of generated proofs and improving the interpretability of the reasoning process. As research in this field progresses, NTPs have the potential to revolutionize automated theorem proving and contribute to advancements in mathematics, formal verification, and artificial intelligence.

3.5.2 A Concrete Example of a Neural Theorem Prover

One concrete example of a Neural Theorem Prover is the “Neural Theorem Prover over Dependency Graphs” (DepGNTP) introduced by Crouse et al. in their 2021 paper titled “Neural Theorem Proving on Dependency Graphs”. Let’s explore this specific implementation in detail:

3.5.2.1 Problem Formulation

DepGNTP focuses on theorem proving in first-order logic (FOL) using dependency graphs. The input to DepGNTP is a FOL problem consisting of a set of axioms and a conjecture to be proved. The axioms and the conjecture are represented as a dependency graph, where nodes represent FOL formulas and edges represent dependencies between the formulas.

3.5.2.2 Architecture

DepGNTP consists of a graph neural network (GNN) and a symbolic reasoning engine. The GNN operates on the dependency graph representation of the FOL problem. The GNN architecture includes graph convolutional layers and attention mechanisms to process the nodes and edges of the dependency graph. The symbolic reasoning engine is responsible for applying logical inference rules and constructing the proof based on the guidance from the GNN.

3.5.2.3 Training

DepGNTP is trained on a dataset of FOL problems and their corresponding proofs. The training data includes the dependency graphs of the FOL problems, where each node is labeled with the corresponding FOL formula. The GNN is trained to predict the next proof step or the relevant axioms and rules to apply at each step of the proof. The training objective is formulated as a classification problem, where the GNN learns to predict the correct action (proof step or axiom/rule selection) based on the current state of the dependency graph.

3.5.2.4 Inference

During inference, DepGNTP takes a new FOL problem as input and constructs the corresponding dependency graph. The GNN processes the dependency graph and predicts the most promising proof steps or axioms/rules to apply at each step. The symbolic reasoning engine applies the selected axioms and rules to construct the proof, following the guidance from the GNN. The inference process iteratively combines the GNN’s predictions with the symbolic reasoning until a complete proof is found or a certain depth limit is reached.

3.5.2.5 Results and Evaluation

The authors evaluated DepGNTP on a dataset of FOL problems from the TPTP (Thousands of Problems for Theorem Provers) library. They compared DepGNTP with a baseline neural theorem prover and a traditional theorem prover (E-Prover). DepGNTP outperformed the baseline neural theorem prover and achieved competitive results compared to E-Prover, demonstrating the effectiveness of combining GNNs with dependency graphs for theorem proving.

3.5.2.6 Advantages and Limitations

DepGNTP leverages the structural information in the dependency graphs to guide the theorem proving process, which can lead to more efficient and accurate proofs. The use of GNNs allows DepGNTP to learn from the patterns and dependencies in the FOL problems and generalize to unseen problems. However, like other NTPs, DepGNTP faces challenges in ensuring the correctness and completeness of the generated proofs. The interpretability of the learned proof strategies and the reasoning process of DepGNTP can be limited, making it difficult to understand and verify the generated proofs.

The “Neural Theorem Prover over Dependency Graphs” (DepGNTP) is a specific implementation of a Neural Theorem Prover that combines graph neural networks with dependency graphs for theorem proving in first-order logic. It demonstrates the potential of leveraging structural information and neural networks to improve the efficiency and effectiveness of automated theorem proving. However, further research is needed to address the challenges of correctness, completeness, and interpretability in NTPs like DepGNTP.

3.5.3 Example of DepGNTP

Let’s show a specific example of how DepGNTP would work. Consider the following FOL problem:

Axioms:

$\forall{x} (Human(x) → Mortal(x))$
$Human(Socrates)$ >

Conjecture:

$Mortal(Socrates)$

Step 1: Dependency Graph Construction

The FOL problem is transformed into a dependency graph representation. Each axiom and the conjecture become nodes in the graph. Edges are added to represent dependencies between the formulas.

Dependency Graph:

Node 1: $∀x (Human(x) → Mortal(x))$
Node 2: $Human(Socrates)$
Node 3: $Mortal(Socrates)$
Edge 1: $Node 1 → Node 3$ (indicating that Node 1 is relevant for proving Node 3)

Step 2: Graph Neural Network Processing

The GNN component of DepGNTP takes the dependency graph as input. It processes the nodes and edges using graph convolutional layers and attention mechanisms. The GNN learns to predict the most promising proof steps or axioms/rules to apply at each step.

GNN Output: The GNN predicts that the next proof step should involve applying axiom 1 $(∀x (Human(x) → Mortal(x)))$ to the conjecture ( $Mortal(Socrates)$ ).

Step 3: Symbolic Reasoning

The symbolic reasoning engine of DepGNTP takes the GNN’s prediction and applies the selected axiom/rule. In this case, it applies axiom 1 to the conjecture using the substitution {x → Socrates}. $\{x → Socrates\}$

Proof Step:

$∀x (Human(x) → Mortal(x))$ [Axiom 1]
$Human(Socrates) → Mortal(Socrates)$ [Universal Elimination from 1]
$Human(Socrates)$ [Axiom 2]
$Mortal(Socrates)$ [Modus Ponens from 2 and 3]

Step 4: Iterative Process

DepGNTP continues the process iteratively, with the GNN predicting the next proof step and the symbolic reasoning engine applying the selected axioms/rules. In this example, the proof is complete after step 4, as the conjecture (Mortal(Socrates)) has been derived.

Final Proof:

$∀x (Human(x) → Mortal(x))$ [Axiom 1]
$Human(Socrates) → Mortal(Socrates)$ [Universal Elimination from 1]
$Human(Socrates)$ [Axiom 2]
$Mortal(Socrates)$ [Modus Ponens from 2 and 3]

In this example, DepGNTP successfully proves the conjecture (Mortal(Socrates)) using the given axioms. The GNN guides the proof process by predicting the most relevant axioms and rules to apply at each step, while the symbolic reasoning engine applies the selected axioms/rules to construct the proof.

Note that this is a simplified example for illustrative purposes. In practice, DepGNTP can handle more complex FOL problems with larger dependency graphs and multiple proof steps. The GNN’s predictions and the symbolic reasoning process become more intricate as the complexity of the problem increases.

3.6 Neural Symbolic Machines

Neural Symbolic Machines (NSMs) are a class of AI systems that combine the strengths of neural networks and symbolic reasoning to enable more interpretable, robust, and generalizable learning. They aim to bridge the gap between the sub-symbolic level of neural networks and the symbolic level of traditional AI systems. Let’s explore Neural Symbolic Machines in more detail:

Overview: NSMs integrate neural networks with symbolic knowledge representation and reasoning. They leverage neural networks for learning and perception while using symbolic techniques for reasoning, knowledge representation, and explanation. The goal is to create AI systems that can learn from data, reason over symbolic knowledge, and provide interpretable explanations for their decisions.

Architecture: NSMs typically consist of three main components:

A neural network
A symbolic knowledge base
An integration module

The neural network component is responsible for perception, feature extraction, and learning from raw data. The symbolic knowledge base stores structured knowledge in the form of ontologies, rules, constraints, or logical formulas. The integration module facilitates the interaction between the neural network and the symbolic knowledge base, enabling the exchange of information and the coordination of reasoning processes.

Learning and Reasoning: NSMs employ various learning mechanisms to acquire knowledge from data and update the symbolic knowledge base. Supervised learning techniques can be used to train the neural network on labeled data, allowing it to learn patterns and extract relevant features. Unsupervised learning methods, such as clustering or dimensionality reduction, can help discover structure and relationships in the data. Reinforcement learning can be employed to learn optimal decision-making policies through interaction with an environment. The learned knowledge is then incorporated into the symbolic knowledge base, either by extracting symbolic rules or by updating existing knowledge. During reasoning, the symbolic knowledge base is used to perform logical inference, constraint satisfaction, or rule-based reasoning over the learned knowledge.

Knowledge Representation: NSMs utilize various knowledge representation formalisms to encode symbolic knowledge. Ontologies provide a structured representation of concepts, relationships, and hierarchies in a domain. Logic-based formalisms, such as first-order logic or description logic, allow for expressive representation of rules, constraints, and axioms. Probabilistic graphical models, such as Bayesian networks or Markov networks, can capture uncertain knowledge and reasoning. The choice of knowledge representation depends on the specific requirements of the application domain and the reasoning tasks at hand.

Explanation and Interpretability: One of the key advantages of NSMs is their ability to provide explanations and interpretability. By combining neural networks with symbolic knowledge, NSMs can generate human-understandable explanations for their decisions and reasoning processes. The symbolic knowledge base acts as a source of interpretable knowledge that can be traced and explained. Explanation techniques, such as rule extraction or attention mechanisms, can be used to highlight the relevant symbolic knowledge used in decision-making. The interpretability of NSMs enhances trust, transparency, and accountability in AI systems.

Applications: NSMs have been applied to various domains, including natural language processing, computer vision, robotics, and recommendation systems. In natural language processing, NSMs can perform tasks such as question answering, semantic parsing, and dialogue systems by combining neural language models with symbolic knowledge bases. In computer vision, NSMs can integrate object recognition and scene understanding with symbolic reasoning to perform tasks like visual question answering and image captioning. In robotics, NSMs can enable robots to learn from demonstrations, reason about actions and goals, and generate explainable plans. In recommendation systems, NSMs can combine user preferences and item features with symbolic knowledge about user-item relationships to provide personalized and explainable recommendations.

Challenges and Future Directions: Integrating neural networks and symbolic reasoning poses several challenges, such as bridging the gap between sub-symbolic and symbolic representations, handling uncertainty and noise, and ensuring the consistency and coherence of the integrated system. Scaling NSMs to large-scale knowledge bases and complex reasoning tasks requires efficient algorithms and representations. Developing effective learning algorithms that can extract meaningful symbolic knowledge from data and update the knowledge base incrementally is an ongoing research area. Enhancing the interpretability and explainability of NSMs, especially in complex domains with large knowledge bases, is crucial for their wider adoption and trust. Exploring the integration of NSMs with other AI paradigms, such as reinforcement learning and transfer learning, can lead to more versatile and adaptable systems.

3.7 Differentiable Reasoning

Differentiable Reasoning is a subfield of machine learning that aims to incorporate structured reasoning and symbolic knowledge into neural networks while maintaining end-to-end differentiability. It enables neural networks to perform logical reasoning, symbol manipulation, and complex decision-making in a way that is compatible with gradient-based optimization. Let’s explore Differentiable Reasoning in more detail:

Motivation:

Traditional neural networks excel at pattern recognition and feature learning but struggle with explicit reasoning and symbol manipulation.
Symbolic AI systems, on the other hand, can perform logical reasoning and handle structured knowledge but lack the flexibility and learning capabilities of neural networks.
Differentiable Reasoning aims to bridge this gap by integrating reasoning capabilities into neural networks while preserving the benefits of end-to-end learning.

Key Concepts:

Differentiable Programming: Differentiable Reasoning builds upon the concept of differentiable programming, where the entire reasoning process is formulated as a differentiable computation graph.
Soft Logic: Instead of using hard logical operations, Differentiable Reasoning employs soft logic, which assigns continuous values to logical expressions, allowing for gradient-based optimization.
Neural Symbolic Representations: Differentiable Reasoning uses neural symbolic representations that encode structured knowledge and symbols into continuous vector spaces, enabling seamless integration with neural networks.

Architectures and Techniques:

Neural Theorem Provers: These architectures combine neural networks with symbolic theorem provers, enabling the learning of logical rules and the generation of proofs through differentiable operations.
Differentiable Inductive Logic Programming (ILP): ILP systems are extended to be differentiable, allowing for the learning of logical rules and the integration of background knowledge into neural networks.
Neural Logic Machines: These architectures use neural networks to implement logical operations and perform reasoning over symbolic knowledge bases.
Differentiable Satisfiability (DSAT) Solvers: DSAT solvers are made differentiable, enabling the integration of constraint satisfaction and optimization within neural networks.

Reasoning Tasks:

Logical Inference: Differentiable Reasoning enables neural networks to perform logical inference, such as deduction, induction, and abduction, by learning and applying logical rules.
Knowledge Base Reasoning: Neural networks can reason over structured knowledge bases, answering queries and deriving new facts through differentiable operations.
Constraint Satisfaction: Differentiable Reasoning allows neural networks to solve constraint satisfaction problems by incorporating differentiable constraints into the learning process.
Planning and Decision Making: Differentiable Reasoning can be used for planning and decision-making tasks, where the reasoning process is guided by learned policies and objective functions.

Challenges and Future Directions:

Scalability: Differentiable Reasoning techniques need to be scaled to handle large-scale knowledge bases and complex reasoning tasks efficiently.
Interpretability: While Differentiable Reasoning aims to improve the interpretability of neural networks, further research is needed to enhance the transparency and explainability of the reasoning process.
Integration with Other AI Paradigms: Exploring the integration of Differentiable Reasoning with other AI paradigms, such as reinforcement learning and unsupervised learning, can lead to more powerful and versatile reasoning systems.
Real-World Applications: Applying Differentiable Reasoning to real-world problems, such as natural language understanding, visual reasoning, and robotic planning, is an important direction for future research.

Applications:

Natural Language Processing: Differentiable Reasoning can be used for tasks such as question answering, semantic parsing, and natural language inference, where reasoning over linguistic structures and knowledge bases is required.
Computer Vision: Differentiable Reasoning can enable visual reasoning tasks such as visual question answering, scene understanding, and object relation reasoning.
Robotics: Differentiable Reasoning can be applied to robotic planning, decision-making, and task execution, where reasoning over symbolic representations and constraints is necessary.
Recommender Systems: Differentiable Reasoning can enhance recommender systems by incorporating logical reasoning and knowledge-based constraints into the recommendation process.

3.7.1 Example: Learning Logical Rules for Family Relationships

Suppose we have a dataset of family relationships, where each data point represents a pair of individuals and their relationship. The goal is to learn logical rules that define these relationships and use them to infer new relationships.

Dataset:

(Alice, Bob, parent)
(Bob, Charlie, parent)
(Alice, Charlie, grandparent)
(David, Eva, parent)
(Eva, Fiona, parent)
(David, Fiona, grandparent)

Step 1: Neural Symbolic Representation

We encode the individuals and relationships into a continuous vector space using an embedding layer. Each individual (e.g., Alice, Bob) is represented by a dense vector, and each relationship (e.g., parent, grandparent) is also represented by a dense vector.

Step 2: Differentiable Logical Rules

We define differentiable logical rules that capture the relationships between individuals. For example, we can define a rule for the grandparent relationship:

grandparent(x, z) :- parent(x, y), parent(y, z)

This rule states that if x is a parent of y, and y is a parent of z, then x is a grandparent of z. We use differentiable operations, such as soft logic or neural arithmetic, to implement these rules.

Step 3: Training

We train the system using the dataset of family relationships. The embedding layer learns to map individuals and relationships to meaningful vector representations.

The differentiable logical rules are optimized to minimize the difference between the predicted relationships and the ground truth. The system learns to assign high probabilities to valid relationships and low probabilities to invalid ones.

Step 4: Inference

After training, we can use the learned logical rules to infer new relationships. For example, given a new pair of individuals (George, Hannah), we can query the system to infer their relationship.

The system applies the learned logical rules to the vector representations of George and Hannah and computes the probability of different relationships.

If the system predicts a high probability for the grandparent relationship, it means that George is likely to be a grandparent of Hannah based on the learned rules.

Step 5: Interpretation and Explanation

One of the benefits of Differentiable Reasoning is the ability to interpret and explain the reasoning process.

We can analyze the learned logical rules and their weights to understand how the system arrives at its predictions.

For example, we can examine the rule for the grandparent relationship and see that it assigns high importance to the parent relationships in the chain. This interpretability helps in understanding the reasoning behind the system’s decisions and enhances trust in the model.

In this example, Differentiable Reasoning enables the learning of logical rules from data and the inference of new relationships based on those rules. The differentiable nature of the reasoning process allows for end-to-end optimization and the integration of symbolic knowledge with neural networks.

4. Graph Neural Networks

Graph Neural Networks (GNNs) and neurosymbolic AI are closely related, as GNNs provide a framework for integrating symbolic reasoning with deep learning on graph-structured data. Neurosymbolic AI aims to combine the strengths of neural networks and symbolic reasoning to create more interpretable, flexible, and generalizable AI systems. In this context, GNNs serve as a bridge between the neural and symbolic domains. Let’s explore the connection between GNNs and neurosymbolic AI in more detail.

Symbolic Reasoning on Graphs:

Graphs are a natural representation for symbolic knowledge, such as ontologies, knowledge bases, and logical rules. GNNs enable the incorporation of symbolic reasoning within deep learning models by operating on graph-structured data. By learning representations of nodes and edges in a graph, GNNs can capture the relational and structural information embedded in the symbolic knowledge.

Reasoning over Knowledge Graphs:

Knowledge graphs are a prominent example of symbolic knowledge representation, where entities are represented as nodes and relations as edges. GNNs have been successfully applied to reasoning tasks over knowledge graphs, such as link prediction, entity classification, and graph completion. By learning expressive representations of entities and relations, GNNs can perform reasoning and inference over the knowledge graph.

Logical Reasoning with GNNs:

GNNs can be extended to incorporate logical reasoning capabilities by integrating symbolic rules and constraints into the learning process. For example, Graph Logic Networks (GLNs) and Logical Neural Networks (LNNs) incorporate logical rules and constraints into the message passing and aggregation steps of GNNs. By enforcing logical consistency during the learning process, these models can perform logical reasoning tasks, such as satisfiability checking and theorem proving.

Interpretability and Explainability:

One of the key goals of neurosymbolic AI is to improve the interpretability and explainability of AI systems. GNNs can contribute to this goal by providing a way to learn interpretable representations of symbolic knowledge. By analyzing the learned node and edge representations, as well as the attention weights and pooling operations, researchers can gain insights into the reasoning process of GNNs. This interpretability can help in understanding the model’s predictions and explaining its behavior.

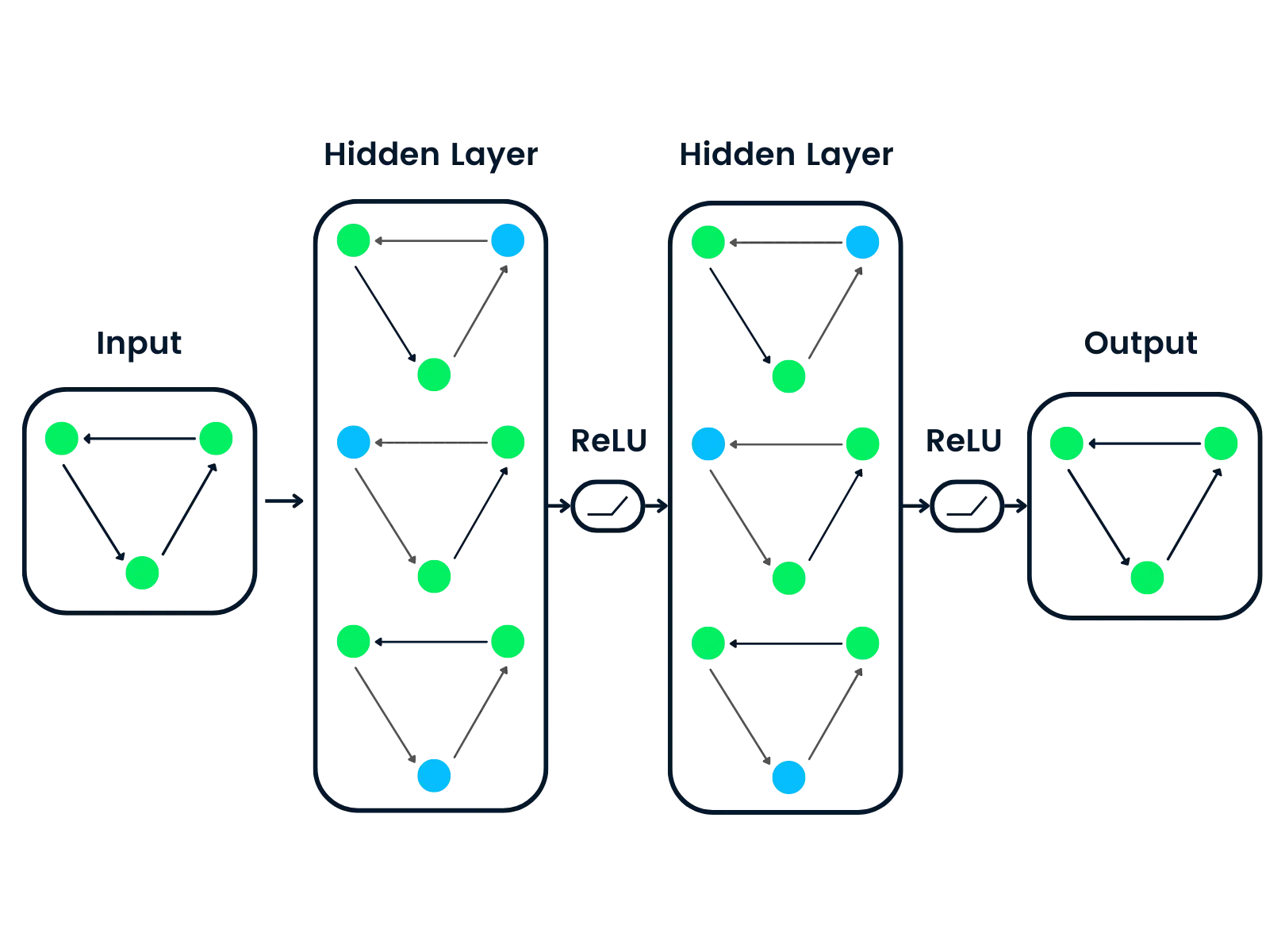
alt text

Diagram 8. An example of a Graph Neural Network using the ReLU activation function.

4.1 GNN Aggregation Functions

There are several aggregation functions commonly used in Graph Neural Networks (GNNs) to combine the messages received by a node from its neighbors. Here are some examples:

Sum Aggregation:

The sum aggregation function simply sums up all the incoming messages to update the node representation. Mathematically, it can be expressed as:

h'j = σ(W_h · h_j + ∑{i ∈ N(j)} m_{ij})

where $h_j$ is the updated representation of node $j$ , σ is a non-linear activation function, $W_h$ is a learnable weight matrix, $h_j$ is the current representation of node j, $m_{ij}$ is the message from node $i$ to node $j$ , and $N(j)$ denotes the set of neighbors of node $j$ .

Mean Aggregation:

The mean aggregation function takes the element-wise mean of the incoming messages to update the node representation. It can be expressed as:

h'j = σ(W_h · h_j + (1 / |N(j)|) ∑{i ∈ N(j)} m_{ij})

where $|N(j)|$ denotes the number of neighbors of node $j$ .

Max Aggregation:

The max aggregation function takes the element-wise maximum of the incoming messages to update the node representation. It can be expressed as:

h'j = σ(W_h · h_j + max{i ∈ N(j)} m_{ij})

where max denotes the element-wise maximum operation.

Attention-based Aggregation:

Attention-based aggregation functions assign different weights to the incoming messages based on their relevance or importance. The weights are typically computed using an attention mechanism, such as the dot product between the node representations. One example is the Graph Attention Network (GAT) aggregation:

h'j = σ(∑{i ∈ N(j)} α_{ij} · W_h · h_i)

where $α_\{ij\}$ is the attention weight computed for the message from node $i$ to node $j$ , and $W_h$ is a learnable weight matrix.

Pooling Aggregation: Pooling aggregation functions apply a pooling operation, such as max pooling or average pooling, to the incoming messages. For example, max pooling aggregation can be expressed as:

h'j = σ(W_h · MaxPool({m{ij} | i ∈ N(j)}))

where MaxPool denotes the max pooling operation applied to the set of incoming messages.

These are just a few examples of aggregation functions used in GNNs. The choice of aggregation function depends on the specific problem and the desired behavior of the GNN model. Researchers continue to explore new and more sophisticated aggregation functions to improve the performance and expressiveness of GNNs.

Choosing the Appropriate Aggregation Function: Choosing the appropriate aggregation function for a specific problem in Graph Neural Networks (GNNs) is an important aspect of model design. Researchers typically consider several factors when determining which aggregation function to use:

Problem Characteristics: The nature of the problem and the specific task at hand play a crucial role in selecting the aggregation function. For example:

For tasks that require capturing the overall information from the neighborhood, such as node classification or graph classification, sum or mean aggregation functions might be suitable.
For tasks that focus on identifying the most important or discriminative features, such as anomaly detection or key node identification, max aggregation or attention-based aggregation could be more appropriate.

Graph Structure and Properties: The structure and properties of the input graph can influence the choice of aggregation function. Researchers consider factors such as:

Graph density: For dense graphs with many connections, mean aggregation or attention-based aggregation might be preferred to avoid overemphasizing high-degree nodes.
Graph heterogeneity: If the graph contains different types of nodes or edges, attention-based aggregation can help in learning the relative importance of different node or edge types.
Graph size: For large-scale graphs, computationally efficient aggregation functions like sum or mean aggregation might be favored over more complex ones.

Model Architecture: The overall architecture of the GNN model can also guide the selection of the aggregation function. For instance:

If the model includes multiple layers of aggregation, using different aggregation functions at different layers can help capture diverse patterns and improve the model’s expressiveness.
If the model incorporates attention mechanisms, attention-based aggregation functions are a natural choice to leverage the learned attention weights.

Empirical Performance: Researchers often experiment with different aggregation functions and evaluate their performance on the specific problem and dataset. They compare metrics such as accuracy, F1 score, or mean squared error to assess which aggregation function yields the best results.

Computational Efficiency: The computational complexity and efficiency of the aggregation function are also considered, especially for large-scale graphs or resource-constrained scenarios. Simpler aggregation functions like sum or mean aggregation are generally more computationally efficient compared to attention-based or pooling aggregations.

Domain Knowledge and Prior Work: Researchers also take into account domain knowledge and insights from prior work in similar problem domains. They may draw inspiration from successful applications of certain aggregation functions in related tasks or datasets.

In practice, researchers often experiment with multiple aggregation functions and compare their performance to make an informed decision. They may also propose novel aggregation functions tailored to the specific requirements of their problem. It’s important to note that the choice of aggregation function is just one aspect of designing effective GNN models, and it should be considered in conjunction with other design choices, such as the number of layers, the choice of activation functions, and the overall model architecture.

4.2 Activation Functions in GNNs

Activation functions play a crucial role in GNNs, as they introduce non-linearity into the model and enable it to learn complex patterns and relationships in the graph data. The choice of activation function can significantly impact the performance and behavior of the GNN model. In this section, we will explore some commonly used activation functions in GNNs and discuss their properties and suitability for different tasks.

ReLU (Rectified Linear Unit): The ReLU activation function is one of the most widely used activation functions in deep learning, including GNNs. It is defined as:

ReLU(x) = max(0, x)

ReLU has several advantages, such as:

It introduces non-linearity while maintaining a simple and computationally efficient form.
It helps alleviate the vanishing gradient problem, as it allows gradients to flow freely for positive inputs.
It promotes sparsity in the learned representations, as it outputs zero for negative inputs.

Leaky ReLU:

Leaky ReLU is a variant of the ReLU activation function that addresses the “dying ReLU” problem, where neurons with negative inputs become permanently inactive. Leaky ReLU is defined as:

LeakyReLU(x) = max(αx, x)

where α is a small positive constant (typically around 0.01). Leaky ReLU allows a small gradient to flow even for negative inputs, helping to prevent neurons from becoming permanently inactive.

ELU (Exponential Linear Unit):

The ELU activation function is another variant of ReLU that aims to address the vanishing gradient problem and improve the learning dynamics. ELU is defined as:

ELU(x) = { x if x > 0 α(exp(x) - 1) if x ≤ 0 }

where α is a hyperparameter that controls the saturation for negative inputs. ELU has the advantage of providing negative outputs, which can help center the activations and improve the learning dynamics.

Softmax: The softmax activation function is commonly used in the output layer of GNNs for tasks that require probability distributions, such as node classification or graph classification. Softmax is defined as:

softmax(x_i) = exp(x_i) / ∑_j exp(x_j)

where $x_i$ is the $i$ -th element of the input vector $x$ . Softmax normalizes the input values into a probability distribution, ensuring that the outputs sum up to one.

When choosing an activation function for a GNN model, researchers consider factors such as the problem domain, the desired properties of the learned representations, and the computational efficiency. Experimentation and empirical evaluation are often conducted to determine the most suitable activation function for a specific task.

It’s worth noting that the activation functions mentioned above are just a few examples, and there are many other activation functions used in GNNs, such as sigmoid, hyperbolic tangent (tanh), and parameterized ReLU (PReLU). Researchers continue to explore new activation functions and variants to improve the performance and stability of GNN models.

4.3 Graph Convolutional Networks

A Graph Convolutional Network (GCN) is a specific type of Graph Neural Network (GNN) that extends the concept of convolution operations to graph-structured data. GCNs are designed to learn node representations by aggregating information from neighboring nodes in a graph.

In a GCN, the convolution operation is applied to the graph, where the node features are updated by aggregating the features of neighboring nodes. The key idea behind GCNs is to learn a function that transforms the features of a node based on the features of its neighbors, allowing for the propagation of information across the graph.

Here’s how GCNs relate to the broader concept of GNNs:

GNNs as a Framework: GNNs provide a general framework for designing neural network architectures that can operate on graph-structured data. GNNs encompass various approaches and architectures, including GCNs, Graph Attention Networks (GATs), Graph Isomorphism Networks (GINs), and others.
Convolution on Graphs: GCNs introduce the concept of convolution operations on graphs. In traditional convolutional neural networks (CNNs), convolution is performed on regular grid-like structures, such as images. GCNs extend this idea to graphs by defining convolution operations that can handle the irregular and non-Euclidean nature of graph-structured data.
Aggregation of Neighboring Features: In a GCN, each node aggregates the features of its neighboring nodes to update its own representation. The aggregation process typically involves a weighted sum of the neighboring features, where the weights are learned during training. This allows the node to incorporate information from its local neighborhood and capture the structural information of the graph.
Multiple Layers: GCNs can have multiple convolutional layers, where each layer aggregates information from a larger neighborhood. By stacking multiple layers, GCNs can capture both local and global patterns in the graph, allowing for the learning of hierarchical representations.
Learning Node Embeddings: The output of a GCN is a set of node embeddings, where each node is represented by a low-dimensional vector that encodes its features and structural information. These embeddings can be used for various downstream tasks, such as node classification, link prediction, or graph classification.
Message Passing Mechanism: GCNs can be seen as a specific instance of the message passing framework in GNNs. The convolution operation in GCNs corresponds to the message passing step, where nodes exchange information with their neighbors to update their representations.
Variants and Extensions: There are various variants and extensions of GCNs, such as Graph Attention Networks (GATs) that incorporate attention mechanisms to weight the importance of different neighbors, or Graph Isomorphism Networks (GINs) that aim to capture isomorphic structures in graphs.

GCNs have been widely applied to various domains, including social network analysis, recommendation systems, molecular property prediction, and more. They have shown great success in tasks that involve learning from graph-structured data and have become a fundamental building block in the field of graph representation learning.

4.4 Defining GCN Convolution Operations

There are two main approaches to defining convolution operations on graphs: spectral and spatial. Spectral approaches operate in the Fourier domain and define convolution using the eigendecomposition of the graph Laplacian matrix. Spatial approaches, on the other hand, define convolution directly on the graph structure by aggregating information from neighboring nodes. Most GCN implementations, such as the popular one proposed by Kipf and Welling (2017), follow the spatial approach due to its computational efficiency and ability to handle large-scale graphs.

Aggregation Functions: The aggregation function in GCNs determines how the features of neighboring nodes are combined to update the representation of a node. Common aggregation functions include mean pooling, sum pooling, and weighted sum pooling. The choice of aggregation function can impact the expressive power and learning dynamics of the GCN. Some variants, like Graph Attention Networks (GATs), introduce attention mechanisms to learn the importance weights of different neighbors during aggregation.

Oversmoothing and Deep GCNs: One challenge in training deep GCNs is the oversmoothing problem, where the node representations become indistinguishable as the number of layers increases. This is because repeated aggregation of neighboring features can lead to a loss of discriminative information. Various techniques have been proposed to mitigate oversmoothing, such as using residual connections, adding normalization layers, or employing adaptive aggregation schemes.

Inductive and Transductive Learning: GCNs can be used for both inductive and transductive learning tasks. In transductive learning, the model is trained and evaluated on the same fixed graph, and the goal is to predict the labels of unlabeled nodes. In inductive learning, the model is trained on a set of graphs and then applied to new, unseen graphs for prediction. Inductive learning requires the GCN to learn transferable and generalizable node representations that can be applied to new graph instances.

4.5 Applications of GCNs

GCNs have been applied to a wide range of domains and tasks. Some notable applications include:

Social Network Analysis: GCNs can be used to predict user attributes, recommend friends or content, or detect communities in social networks.
Recommender Systems: GCNs can capture the complex relationships between users, items, and their interactions in recommendation tasks.
Molecular Property Prediction: GCNs can learn representations of molecules and predict their properties, such as toxicity or binding affinity, based on their graph structure.
Traffic Forecasting: GCNs can model the spatial and temporal dependencies in traffic networks to predict traffic congestion or demand.
Computer Vision: GCNs have been used for tasks like image classification, semantic segmentation, and action recognition by representing images as graphs.

Scalability and Efficiency: One of the challenges in applying GCNs to large-scale graphs is the computational complexity of the convolution operation, which requires aggregating information from all neighboring nodes. Various techniques have been proposed to improve the scalability and efficiency of GCNs, such as graph sampling, subgraph batching, and approximation techniques like FastGCN or GraphSAGE.

Integration with Other Architectures: GCNs can be combined with other neural network architectures to create more powerful and specialized models. For example, GCNs can be integrated with recurrent neural networks (RNNs) to handle temporal graphs, or with convolutional neural networks (CNNs) to process grid-like structures within graphs.

4.6 Graph Pooling Techniques in GCNs

Graph pooling is an essential operation in GCNs that aims to reduce the size of graph representations while preserving important structural and feature information. Pooling allows GCNs to capture hierarchical patterns and learn more abstract representations of the graph data. In this section, we will explore various graph pooling techniques used in GCNs and discuss their properties and applications.

Global Pooling: Global pooling techniques aggregate node representations from the entire graph into a single graph-level representation. Some common global pooling methods include:

Max Pooling: Applies element-wise maximum operation to the node representations.
Average Pooling: Computes the element-wise average of the node representations.
Sum Pooling: Performs element-wise summation of the node representations. Global pooling is computationally efficient and can be used for tasks that require graph-level predictions, such as graph classification or graph regression.

Hierarchical Pooling: Hierarchical pooling techniques aim to generate a hierarchical representation of the graph by repeatedly clustering or coarsening the nodes. Some popular hierarchical pooling methods include:

DiffPool: Differentiable pooling operator that learns a soft cluster assignment matrix to pool nodes into clusters.
TopKPool: Selects the top-k nodes based on a learnable scoring function and performs pooling on the selected nodes.
SAGPool: Self-Attention Graph Pooling, which uses a self-attention mechanism to learn the importance of nodes and performs pooling based on the learned scores.

Hierarchical pooling allows GNNs to capture multi-scale information and can be particularly useful for tasks that benefit from hierarchical graph representations.

Edge Pooling: Edge pooling techniques focus on aggregating information from edges rather than nodes. They can be useful in scenarios where edge attributes carry significant information. Some edge pooling methods include:

Edge Contraction Pooling: Contract edges based on a learnable edge scoring function and merges the connected nodes.
Edge Attention Pooling: Applies attention mechanisms to learn the importance of edges and performs pooling based on the learned attention weights.

Edge pooling can help capture important edge-level patterns and can be particularly relevant for tasks involving edge prediction or edge classification.

Hybrid Pooling: Hybrid pooling techniques combine multiple pooling methods to leverage their complementary strengths. For example:

Global-Attention Pooling: Combines global pooling with attention mechanisms to learn the importance of nodes or edges.
Hierarchical-Edge Pooling: Integrates hierarchical pooling with edge pooling to capture both node-level and edge-level patterns.

Hybrid pooling can provide more flexible and expressive graph representations by combining different pooling strategies.

Adaptive Pooling: Adaptive pooling techniques dynamically adjust the pooling operation based on the graph structure and input features. Some adaptive pooling methods include:

Graph U-Net: Adopts the U-Net architecture with adaptive pooling and unpooling operations to learn hierarchical graph representations.
Dynamic Graph Pooling: Adjusts the pooling operation based on the learned importance scores of nodes or edges, allowing for adaptive graph coarsening.

Adaptive pooling can improve the model’s ability to capture diverse patterns and adapt to different graph structures.

4.7 Conclusion on GNNs and Pooling

Graph Neural Networks (GNNs) are powerful tools for learning from graph-structured data, with Graph Convolutional Networks (GCNs) being a prominent subclass of GNNs. GCNs extend the concept of convolution operations to graphs, allowing for the aggregation of neighboring node features to learn expressive node representations.

The choice of aggregation function and activation function in GCNs plays a crucial role in determining the model’s performance and behavior. Common aggregation functions include sum pooling, mean pooling, max pooling, and attention-based pooling, each with its own strengths and applications. Activation functions like ReLU, Leaky ReLU, ELU, and softmax introduce non-linearity into the model and enable it to learn complex patterns and relationships in the graph data.

Graph pooling techniques further enhance GCNs by reducing the size of graph representations while preserving important structural and feature information. Global pooling, hierarchical pooling, edge pooling, hybrid pooling, and adaptive pooling methods provide various ways to capture multi-scale and hierarchical patterns in the graph data.

By leveraging the power of GCNs, aggregation functions, activation functions, and pooling techniques, researchers and practitioners can design effective GNN models for a wide range of applications, including social network analysis, recommender systems, molecular property prediction, traffic forecasting, and computer vision.

Future research in GNNs and pooling techniques will continue to explore new architectures, aggregation functions, activation functions, and pooling methods to improve the scalability, efficiency, interpretability, and performance of GNN models. As GNNs become more advanced and versatile, they hold the potential to revolutionize various domains and enable new discoveries and applications in graph-structured data analysis.

5. Applications of Neurosymbolic AI

Neurosymbolic AI has the potential to revolutionize various domains by combining the strengths of neural networks and symbolic reasoning. In this section, we will explore some of the key applications of neurosymbolic AI across different fields.

5.1 Natural Language Processing (NLP)

In the field of NLP, neurosymbolic AI can enhance tasks such as:

Question Answering: By integrating neural language models with symbolic reasoning, neurosymbolic AI can provide more accurate and interpretable answers to complex questions.
Semantic Parsing: Neurosymbolic AI can improve the extraction of structured meaning from unstructured text by combining neural networks’ ability to understand context with symbolic knowledge representations.
Dialogue Systems: Integrating symbolic reasoning into neural dialogue models can enable more coherent and context-aware conversations, as well as provide interpretable explanations for responses.

5.2 Computer Vision

In the domain of computer vision, neurosymbolic AI can enhance tasks such as:

Object Recognition: By incorporating symbolic knowledge about object relationships and attributes, neurosymbolic AI can improve the accuracy and interpretability of object recognition systems.
Scene Understanding: Neurosymbolic AI can enable better understanding of complex scenes by combining visual features learned by neural networks with symbolic reasoning about scene components and their relationships.
Visual Question Answering: Integrating symbolic reasoning with neural visual representations can improve the accuracy and explainability of answers to questions about images.

5.3 Robotics

In the field of robotics, neurosymbolic AI can enhance tasks such as:

Planning and Decision Making: By combining neural networks’ ability to learn from experience with symbolic reasoning about goals and constraints, neurosymbolic AI can enable more flexible and adaptive robotic planning and decision making.
Task Execution: Integrating symbolic reasoning into neural control models can improve the reliability and interpretability of robotic task execution, as well as enable robots to reason about their actions and goals.
Human-Robot Interaction: Neurosymbolic AI can enhance human-robot interaction by enabling robots to understand and reason about human intentions, as well as provide interpretable explanations for their actions.

5.4 Healthcare

In the healthcare domain, neurosymbolic AI can enhance tasks such as:

Diagnosis and Treatment: By combining neural networks’ ability to learn from medical data with symbolic reasoning about medical knowledge and guidelines, neurosymbolic AI can improve the accuracy and interpretability of diagnosis and treatment recommendations.
Medical Image Analysis: Integrating symbolic reasoning with neural medical image analysis models can improve the accuracy and explainability of medical image interpretations.
Clinical Decision Support: Neurosymbolic AI can enhance clinical decision support systems by combining neural networks’ ability to learn from patient data with symbolic reasoning about clinical guidelines and best practices.

5.5 Finance

In the finance domain, neurosymbolic AI can enhance tasks such as:

Fraud Detection: By integrating symbolic reasoning about known fraud patterns with neural networks’ ability to detect anomalies in financial data, neurosymbolic AI can improve the accuracy and interpretability of fraud detection systems.
Risk Assessment: Neurosymbolic AI can enhance risk assessment models by combining neural networks’ ability to learn from historical data with symbolic reasoning about risk factors and relationships.
Algorithmic Trading: Integrating symbolic reasoning into neural trading models can improve the reliability and interpretability of trading decisions, as well as enable more flexible and adaptive trading strategies.

5.6 Education

In the education domain, neurosymbolic AI can enhance tasks such as:

Intelligent Tutoring Systems: By combining neural networks’ ability to learn from student interactions with symbolic reasoning about pedagogical knowledge and teaching strategies, neurosymbolic AI can provide more personalized and effective tutoring.
Educational Content Analysis: Neurosymbolic AI can improve the analysis and generation of educational content by integrating symbolic knowledge about curriculum and learning objectives with neural language models.
Student Assessment: Integrating symbolic reasoning into neural assessment models can improve the accuracy and interpretability of student assessments, as well as enable more flexible and adaptive assessment strategies.

5.7 Summary of Applications

Neurosymbolic AI holds the potential to revolutionize various domains by combining the strengths of neural networks and symbolic reasoning. By integrating neural learning with symbolic knowledge and reasoning, neurosymbolic AI can provide more accurate, interpretable, and reliable solutions to complex problems. The applications discussed in this section highlight the diverse range of fields that can benefit from neurosymbolic AI, from natural language processing and computer vision to robotics, healthcare, finance, and education.

As research in neurosymbolic AI continues to advance, we can expect to see even more innovative and impactful applications across different domains. The future of AI lies in the synergy between neural networks and symbolic reasoning, and neurosymbolic AI represents a promising direction toward achieving more robust, explainable, and trustworthy AI systems.

6. Conclusion

Neurosymbolic AI represents a promising direction in the field of artificial intelligence, combining the strengths of neural networks and symbolic reasoning to create more robust, interpretable, and generalizable AI systems. By integrating the learning and representation capabilities of neural networks with the reasoning and abstraction capabilities of symbolic AI, neurosymbolic AI has the potential to address some of the key challenges facing current AI systems.

In this primer, we have explored the foundations, architectures, and applications of neurosymbolic AI. We have discussed the key concepts and techniques that underlie this exciting field, including symbolic AI techniques, neural networks, graph neural networks, and differentiable reasoning. We have also highlighted the wide range of potential applications across various domains, from natural language processing and computer vision to robotics, healthcare, finance, and education.

As research in neurosymbolic AI continues to advance, we can expect to see even more innovative and impactful applications that leverage the synergy between neural learning and symbolic reasoning. The future of AI lies in the integration of these two paradigms, and neurosymbolic AI represents a significant step toward achieving more explainable, adaptable, and trustworthy AI systems.

By embracing the principles of neurosymbolic AI, we can unlock new possibilities in artificial intelligence and create AI systems that are not only powerful and efficient but also transparent and reliable. The journey of neurosymbolic AI is just beginning, and the potential for transformative advancements in AI is immense.

We hope this primer has provided a comprehensive introduction to neurosymbolic AI and inspired further exploration and research in this exciting field. As we move forward, let us continue to build upon the foundations of neurosymbolic AI and work toward a future where AI systems can learn, reason, and interact with the world in ways that are both intelligent and interpretable.

References

[1] Kipf, T. N., & Welling, M. (2017). Semi-Supervised Classification with Graph Convolutional Networks. arXiv preprint arXiv:1609.02907.
[2] Velickovic, P., Cucurull, G., Casanova, A., Romero, A., Lio, P., & Bengio, Y. (2018). Graph Attention Networks. arXiv preprint arXiv:1710.10903.
[3] Hamilton, W., Ying, R., & Leskovec, J. (2017). Inductive Representation Learning on Large Graphs. Advances in Neural Information Processing Systems (NeurIPS).
[4] Battaglia, P. W., Hamrick, J. B., Bapst, V., Sanchez-Gonzalez, A., Zambaldi, V., Malinowski, M., … & Pascanu, R. (2018). Relational inductive biases, deep learning, and graph networks. arXiv preprint arXiv:1806.01261.